Recall & Precision
Die Qualität von Indexierungsergebnissen beeinflusst wesentlich die Qualität der Informationswiedergewinnung. Dabei werden zwei Größen unterschieden:
- Recall: Wieviele Dokumente werden durch die Recherche gefunden?
- Präzision: Sind die gefundenen Dokumente relevant für die Recherche?
Um eine absolute Vergleichsgröße zu gewinnen, wird ein Einheitsmaß berechnet. Es hängt von dem individuellen Anliegen des Informationssuchenden ab, welche der beiden Größen, Recall oder Präzision, ihm wichtiger ist. Entsprechend kann die eine bzw. die andere Größe bei der Berechnung des Einheitsmaßes mehr oder weniger betont werden.
Zum besseren Verständnis sehen Sie sich bitte folgende Grafik für die Mengen A, B, C, D an:
A = Anzahl der relevanten Datensätze, die bei einer Recherche gefunden wurden
B = Anzahl der nicht relevanten Datensätze, die bei einer Recherche gefunden wurden
C = Anzahl der relevanten Datensätze, die bei einer Recherche nicht gefunden wurden
D = Anzahl der nicht relevanten Datensätze, die bei einer Recherche nicht gefunden wurden 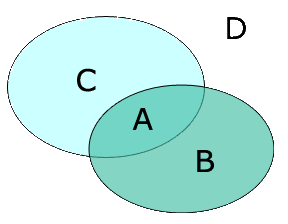
Berechnung der Trefferquote (Recall)
Anteil der gefundenen Datensätze in Relation zu allen Datensätzen, d.h. wieviel % von den Datensätzen, die hätten gefunden werden müssen, wurden überhaupt gefunden?
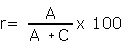
Die Formel für die Berechnung von Recall ohne Prozentangabe ist entsprechend:
r = A / (A + C)
Berechnung der Präzision (Precision)
Anteil der gefundenen relevanten Datensätze in Relation zu allen Datensätzen, die gefunden wurden in %, d.h. wieviel von den gefundenen Datensätzen sind überhaupt nützlich?
p = Berechnung von Präzision
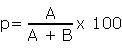
Die Formel für die Berechnung von Präzision ohne Prozentangabe ist entsprechend:
p = A / (A + B)
Berechnung des Einheitsmaßes
Recall und Präzision können zu einem Einheitsmaß kombiniert werden: e= r x p. Je näher dieser Wert an 1 liegt, desto näher kommt er dem Ideal einer 100-prozentigen Recallrate bei gleichzeitig 100-prozentiger Präzisionsrate.
Bei dem Einheitsmaß kann man zusätzlich entweder dem Kriterium Recall oder dem Kriterium Präzision durch den Gewichtungsfaktor b ein höheres Gewicht einräumen. Setzt man z.B. b = 2, legt man ein doppelt so großes Gewicht auf den Recall. Setzt man b = 0.5, legt man ein doppeltes Gewicht auf die Präzision im Information Retrieval.
e liegt hier auch zwischen 0 und 1. e = 0 ist der angestrebte Idealwert, nach dem alle relevanten und nur die relevanten Datensätze wiedergewonnen wurden. e = 1 bedeutet: Kein einziger relevanter Datensatz wurde gefunden.
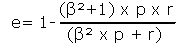
b = Gewichtungsfaktor
r = Recall (nicht in %)
p = Präzision (nicht in %)
Quelle: Vereinfacht nach Grummann, S. 301
2. ZIPFSCHES GESETZ
Die Formeldarstellung für das ZIPFSCHE GESETZ lautet: C = R x A
R = Rang eines Wortes in Häufigkeitsliste (bezogen auf einen Text)
A = Anzahl eines Wortes im Text
C = Konstante
3. Ermittlung der Termfrequenz
Die Häufigkeit eines Wortes in einem Dokument ist also ein Indikator dafür, wie repräsentativ es für den Inhalt des Gesamtdokuments ist. Eine Maßeinheit für das Gewicht eines Wortes in einem Dokument ist die relative Worthäufigkeit (Termfrequenz = TF). Die Termfrequenz (= TF) lässt sich mit einer einfachen Formel errechnen:
TF(td)= Häufigkeit eines Wortes im Dokument |
Abkürzungen:
t = Term
d = Dokument
TF = Termfrequenz
Schauen Sie sich an folgenden Beispielen an, was die Ermittlung der relativen Worthäufigkeit bewirkt.
|
Beispiel 1:
Beispiel 2:
|
Verfeinerung der Formel:
Bei langen Texten erhält man also Werte mit sehr vielen Nullen hinter dem Komma. Um einen engeren Ergebnisbereich für die ermittelten relativen Häufigkeiten zu erhalten, arbeitet man mit logarithmischen Werten. Damit kurze Texte nicht überproportional ins Gewicht fallen, wird zudem im Zähler 1 addiert.
Zur Erinnerung an den Mathematikunterricht:
Logarithmus auf der Basis 2 (Logarithmus dualis): Man nennt die Zahl, mit der man 2 potenzieren muss, damit man 16 erhält, log2 von 16 = 4.
In einem Tabellenkalkulationsprogramm wie Excel finden Sie eine eigene Funktion für die Errechnung des Logarithmus dualis vor.
Termgewicht = log2 (Häufigkeit von t in d + 1)
|
Ergebnisse nach der neuen Formel:
Beispiel 1:
= log2 (5 + 1)/log 2 196 = 0,34
Beispiel 2:
= log 2 (7 +1) /log 2 50.673 = 0,19
Relevanz Ranking
Das Relevanz Ranking lässt sich nach einer einfachen Formel berechnen; natürlich wird in der Praxis mit komplexeren Formeln experimentiert. Schauen Sie sich dazu folgendes Beispiel an.
Gesucht sind Dokumente zum Thema "Tiere und Pflanzen in Korallenriffs" in einer großen biologischen Datenbank mit 1.000.000 Datensätzen.
Die Datenbank enthält
- 40.000 Datensätze mit dem Wort 'Tiere'
- 30.000 Datensätze mit dem Wort 'Pflanzen'
- 50 Datensätze mit dem Wort 'Korallenriffs'
- 10 Datensätze mit Wort 'Seeanemone'
In dem folgenden Beispiel wurde mit dem sogenannten natürlichen Logarithmus (= zur Basis 2,718..) gearbeitet. Auf dem Taschenrechner die Taste ln.
| G = log(N/n) |
- N = eine Konstante, die mindestens so groß ist wie die Anzahl der Treffer für das häufigste Wort in der Datenbank und nicht größer als die Anzahl ihrer Datensätze: also 1.000.000
- n = Anzahl der Treffer für den jeweiligen Suchterminus
In diesem Beispiel:
- Tiere: log(1.000.000 / 40.000) = log 25 = 3,2 (abgerundet)
- Pflanzen: log(1.000.000 / 30.000) = 3,5 (abgerundet)
- Korallenriff: log(1.000.000 / 50) = 9,9 (abgerundet)
- Seeanemone: log( 1.000.000 / 10) = 11,51 (abgerundet)
Für jeden Datensatz, der einen oder mehrere der Suchtermini enthält, werden folgende Schwellenwerte berechnet:
- MAG = minimal akzeptable Gewichtung. Diesen Schwellenwert muss der Datensatz überschreiten, um überhaupt für die Recherche als relevant angezeigt zu werden.
- MMG = maximal mögliche Gewichtung - kann ein Datensatz erhalten, wenn alle Suchtermini in ihm enthalten sind.
Formeln für die Gewichtung der Datensätze
- Für Suchfomulierungen mit nur 1 Suchterminus:
- Für Suchfomulierungen mit genau 2 Suchtermini:
- Für Suchformulierungen mit > 2 Suchtermini
| MAG = MMG |
a) 2 häufig vorkommende Termini (z.B. Tiere von Pflanzen)
| MAG = Summe der Gewichte beider Suchtermini |
b) 1 häufig vorkommender und 1 selten vorkommender Terminus (z.B. 'Tiere im Korallenriff')
| MAG = Gewicht des seltenen Suchterminus |
c) 2 selten vorkommende Suchtermini (z.B. 'Korallenriff und Seeanemone')
| MAG = Gewicht von einem der beiden Suchtermini |
| MAG = MMG / 2 |
Bezogen auf das Beispiel oben: "Tiere und Pflanzen in Korallenriffs": Es handelt sich um eine Suchformulierung mit mehr als 2 Suchtermini.
| MMG = 3,2 + 3,5 + 9,9 = 16,6 |
| MAG = MMG / 2 = 16,6 / 2 = 8,3 |
Folglich werden erst alle Treffer angezeigt,
- die alle Suchtermini enthalten (MMG)
- dann alle Datensätze mit 'Korallenriffs + Pflanzen' (Gewichtung = 13,4)
- dann Datensätze mit 'Korallenriff + Tiere' (Gewichtung = 13,1)
- dann alle Datensätze mit 'Korallenriff' (Gewichtung = 9,9).
- Nicht mehr angezeigt werden Datensätze mit einer Gewichtung unter 8,3 (MAG), also alle Datensätze mit 'Tiere + Pflanzen' (3,2 + 3,5 = 6,7)
Aufgabe von Informationsspezialisten ist es, bei der Erstellung von Informationssystemen auszuprobieren, nach welchen Vorgaben jeweils gewichtet werden soll. So wird man anders gewichten, je nachdem, ob man mehr Wert auf Recall oder auf Precision der Ergebnisse legt.
(Quelle: Stephen Walker; Richard M. Jones: Improving subject retrieval in online catalogues 1. - London : The British Library Board, 1987. - (British Library research paper ; 24). - Kap. 6.5.3., S. 80-82)
Die Dokument-Deskriptor-Matrix
Die Ähnlichkeit zwischen zwei Objekten wird als Funktion der Anzahl der Eigenschaften berechnet, die beiden Objekten gemeinsam sind. Eine Gemeinsamkeit von Dokumenten kann die Zuordnung von Deskriptoren zu diesen Dokumenten sein. Häufig werden auch Hyperlink-Verweise, das Vorkommen bestimmter Wörter im URL oder im Titel zur Ermittlung der Ähnlichkeit herangezogen.
Die Zuordnung von Deskriptoren zu einem Dokument lässt sich gut in Form einer Tabelle vorstellen. In ihrer einfachsten, binären, Form kann man in einer solchen Tabelle festhalten, ob ein Dokument einen Deskriptor enthält oder nicht.
| Deskriptor | Dok 1 | Dok 2 | Dok 3 | Dok 4 |
| Bundeskanzler | 0 | 1 | 0 | 1 |
| Birne | 1 | 1 | 1 | 1 |
| Deutsche Einheit | 1 | 1 | 0 | 1 |
| Euro | 1 | 0 | 1 | 1 |
| Helmut Kohl | 1 | 0 | 1 | 1 |
Das Dokument 1 wird durch die in der Spalte Dok 1 angefügten Deskriptoren repräsentiert. Diese Spalte kann man auch in Form eines Vektors mathematisch darstellen. Die Ähnlichkeit zwischen zwei Vektoren, in unserem Fall also Repräsentanten für zwei Dokumente, kann man ermitteln, wenn man die beiden Vektoren miteinander multipliziert. Für die Multiplikation wird jeder Wert innerhalb eines Vektors mit dem entsprechenden Wert des anderen Vektors multipliziert. Die Werte werden also paarweise multipliziert. Es können nur Vektoren mit derselben Anzahl Dimensionen miteinander multipliziert werden. Als Ergebnis entsteht ein neuer Vektor. Die einzelnen Werte innerhalb des Vektors können anschließend zu einem Ergebnis addiert werden. Wir können jetzt ausrechnen, ob Dokument 4 oder Dokument 2 eine größere Ähnlichkeit zu Dokument 1 aufweist, indem wir die Dokumente paarweise miteinander multiplizieren.
Das Skalarprodukt von Dok 1 und Dok 4 errechnet man also nach folgender Formel:
4 = 0*1 + 1*1 + 1*1 + 1*1 +1*1
Aus dem Ergebnis können wir schließen, dass Dok 1 und Dok 4 sich ähnlicher sind als Dok 1 und Dok 2.
Die gängige mathematische Formeldarstellung für dieses sogenannte Skalarprodukt sieht so aus:
| |
Dieses Wissen reicht bereits aus, um mit Vektoren rechnen zu können und auf diese Weise Änhlichkeiten zwischen Dokumenten zu errechnen.
2. Das Vektorraummodell
Diese Ähnlichkeitsfunktion wird in der Fachliteratur als Vektorraummodell bezeichnet.
Mit Vektoren wird vor allem in der Physik gearbeitet. Es gibt physikalische Größen, wie z. B. die Temperatur, die sich durch eine Zahl ausdrücken lassen. Andere Größen bestehen aus mehreren Werten: So hat die auf einen Körper ausgeübte Kraft eine Richtung und eine Stärke. Solche Größen nennt man Vektoren. Ein Vektor kann aus beliebig vielen Merkmalen bestehen.
Auch die in den Spalten der Dokument-Deskriptor-Matrix festgehaltenen Dokumente lassen sich mathematisch als Vektoren darstellen. Die Deskriptoren bilden die Dimensionen des Vektorraums. Wenn für ein Dokument 5 Deskriptoren bestimmt werden, besitzt der Vektor des Dokuments 5 Dimensionen (n=5). 5 Dimensionen sind für uns graphisch nicht mehr umsetzbar. In der folgenden Präsentation oder in den aufgeführten Links können Sie sich einige Beispiele für Visulisierungen des Modells ansehen. Aus Gründen der Darstellbarkeit müssen sich die Visualisierungen auf drei Dimensionen beschränken.
Stand: 04. April 2011